The Best and Most Useful Lie
The Reality and Unreality of Calculus
by Scooper
2000, retitled 2005
We're going to make the lie true. - Tennesee Williams, Cat on a Hot Tin Roof, 1955
At a web site devoted in large part to the ethics of honesty over and against the ethics of moral purity, it is only fair to acknowledge the limits of honesty itself. After all, complete honesty requires complete self-insight, which none of us has unless it is a gift of God. Besides, sometimes something less than honesty can have great practical value, especially in applied mathematics.
Now mathematics itself can't lie, because it is its own context. It is a language that, if you follow its grammatical rules, guarantees truth, because it only talks about itself. The lie comes in the misapplication of mathematics to real-world situations. Or as Disraeli once said, "There are lies, damned lies, and statistics." But let's skip statistics and get right to the root of it all - calculus, the subject I think every college freshman should study.1
Calculus, especially differential calculus, is used to model almost all the physics we know. This modeling is based on the idea that we can evaluate a function of position and time at points that are arbitrarily close to each other. Suppose for example that we do not know the value of a function at point B, but we do in the region around B. We simply keep picking points A closer and closer to point B, and note the trend in the value of the function we're interested in. This is called taking the limit of our function as point A approaches point B.
To be concrete about this, suppose you wrote down the times you passed certain distance markers as you drove down the highway. For our function we could take the distance between any two markers (in miles or kilometers) and divide by the time (in hours) it took you to drive between the markers, giving your speed in either miles or kilometers per hour. That would give us your average speed between the markers. To get your instantaneous speed, we would have to measure your position at two points infinitesmally close together and divide by the infinitesmally small time interval it took you to go between them. While this may present a problem for actual measurement, it's no problem for mathematics.
Now, as long as we have gone this far, we could take the difference between your instantaneous speeds at two infinitesmally close points along the road, divide by the infinitesmally small time interval it took you to pass from one to the other and get your instantaneous acceleration - the instantaneous change in your instantaneous speed (in miles or kilometers per hour per hour). It is this instantaneous acceleration that Newton was referring to when he wrote "F=ma," or "force equals mass times acceleration," the equation upon which all our physics, directly or indirectly, is based.
The problem is that these limits as one point gets infinitesmally close to another don't really exist. The existence of such a limit presupposes that space and time have no gaps - that they are continuous - which means that you can go smoothly from point A to point B without encountering any holes in the "fabric" of space and time. In fact, the requirements are more stringent: also disallowed are creases, kinks, knots, edges, passageways like the holes in a sponge, etc. For the notion of limits (on which calculus depends) to be valid, the ride from A to B must be much smoother that it possibly can be.
Of course, you don't notice rough spots in space and time while driving your car or walking down the street, because they are quite small, much smaller than an atomic nucleus, or even a sub-atomic particle. But we suspect they're there, because of the probable existence of quantum gravitational zero-point oscillations, the so-called "spacetime foam" mentioned in a previous essay.2 Such a foam may seem smooth to say, a sub-atomic particle, but would be far too rough for calculus to be valid all the way down to infinitesmally small scales.
Another reason I suspect the calculus of being invalid is macroscopic, the so-called Einstein-Poldosky-Rosen paradox,3 which begins like this. Suppose you had a sub-atomic particle that had no intrinsic angular momentum, or spin. Further suppose the particle decays into two more "daughter" particles, each of the same mass, that move apart because of the energy released by the decay. Conservation of linear momentum guarantees that the particles move in opposite directions at equal speeds. And conservation of angular momentum guarantees that each particle would spin in the direction opposite that of the other, so that the two spins would cancel each other out if the particles could be brought back together.
Now, according to our understanding of quantum mechanics, the axis about which the daughter particles spin does not come into existence until a measurement of the spin is made. (This is also a statement about the isotropy of the universe - since space is the same in all directions, there is no preferred axis about which the particles will spin.) The spin of the particle is a potential quantity, which gets made actual by the act of measurement.
And here is the paradox: The other particle, whose axis of spin is also undetermined, instantaneously assumes an equal and opposite spin about the same axis as the first particle measured, regardless of how far away the measurement was made. This appears to violate the principle of Special Relativity that no signal can travel faster than the speed of light.
The paradox is resolved by claiming that neither of the particles by itself forms a complete quantum mechanical system. The system is non-local, which means that until the measurement is made, the two particles are actually one quantum mechanical object. After the measurement, they are each a separate and complete system.
This non-locality is a nice bit of philosophical reasoning, and it's well supported by theory (the work of John S. Bell, among others) and experiment (particularly those of Alain Aspect and co-workers). But in order to make quantum mechanics conform rigorously to Special Relativity I think we need to go further.
In particular, a principal (albeit largely esthetic) tenet of the so-called "Einstein Programme" for theoretical physics is that all physics is local physics, and that all interactions are local interactions. This "locality principle" implies that there must be some sense in which the distance between the two particles in the "non-local" state is actually zero. Allow me to leap from science into speculation.
The particles in the "non-local state" are clearly separated by some distance in three-dimensional space (actually four-dimensional space-time). Perhaps the non-local state of the particles itself creates a bridge between them in one or more other dimensions, which collapses when a measurement is made on either one of them. The total separation between them would then have to be reckoned according to a five- or higher-dimensional formula, which would give zero, even though the three-dimensional part that we're currently aware of is much greater than zero. Figure 1 below shows a cartoon image of this concept. 4
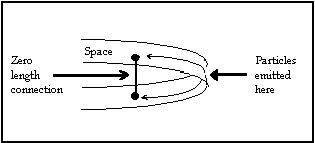
Figure 1. Diagram illustrating a speculative interpretation of the EPR thought experiment. When the spin of either particle of the pair is observed, the quantum mechanical state "collapses" and the higher-dimensional zero-length topological connection between them is broken. The curved "strip of paper" in the figure is meant to represent three-dimensional space. Time is represented by the tracks of the particles, positions since their emission from the parent-particle decay process.
The existence of such a bridge would mean that little higher-dimensional pathways spring up and disappear all the time in our universe, which brings us back to the calculus. The universe may be too swiss-cheesy with sub-microscopic higher-dimensional holes for the smoothness requirments of calculus to be met. In other words, the idea that calculus actually describes reality is a lie.
But it's a good one, because it's so very nearly true that we didn't notice any problems with it for three hundred years. For the most part we still don't notice. We can calculate orbits that get people to the moon and back with calculus. We figured out electromagnetism with it, which gave us radios, televisions, computers, Walkmans, and so much more. And I guarantee that a more accurate theory will be much harder (if not impossible) to use for solving the problems for which calculus works well.
In conclusion, I can say that our mathematics is not so much a map of reality as a metaphor for it. Our current metaphor, the calculus, has such a grip on our imaginations that we physicists will do almost anything to save it, including inventing Supersymmetric String Theories.5 But for practical purposes thus far, calculus is extremely powerful and convenient. If it is ultimately a lie to describe physical reality with it, it is the best and most useful one ever told.
Notes
- See, Teach Your Children.
- See, Science and Faith.
- The most complete discussion I know of this "thought experiment" is in John S. Bell's Speakable and unspeakable in quantum mechanics, Cambridge University Press, 1987. Since most of the discussions are somewhat technical, I recommend you check it out of the library rather than buy it, unless you've already taken an undergraduate course in quantum mechanics.
- For the physicists in the readership, this means that I think that the "collapse of the wavefunction" may be linked to topology change for the case of non-local states. The dimensionality of the "bridge" is equal to the number of non-local quantum numbers describing the state. Janet B. Jones-Oliviera pointed out to me that this type of topology change is fundamentally irreversible. I wonder if any of this might imply altering current methods for calculating Feynman diagrams.
- String theories were invented because taking the limit as point A goes to point B causes certain physical quantities like the self-energy of a point-like particle to become infinite. Although there are mathematically well established ways to handle these infinities in most field theories, they don't work with gravity. Therefore the current rage in physics is to do away with the notion of point-like particles and to pretend that all fundamental particles are closed loops, or strings. This fixes the immediate problem of the infinities, but still hasn't yielded a practical theory. I think this is because the "foaminess" of spacetime at this level has yet to be addressed with a mathematics that has no "points" (or point-substitutes) at all unless some physics makes them happen. Actually, space-time may be "foamy" (multiply connected) even at the macroscopic level, if my speculation regarding the Einstein-Poldosky-Rosen thought experiment has any substance to it.
